Linear regression is a very important concept of machine learning. It helps in finding the relationship between the independent variables and dependent variable

As for the definition of Linear Regression. It can be defined as a statistical method used to model the relation between the dependent variable (Y) and one or more independent variables (X).

There are two types of linear regression:
1. Simple Linear Regression
2. Multiple Linear Regression

Example: Suppose you have to buy a house and its price is defined per square foot. You have collected the data from various agents and now you want to predict the prices of houses in your preferred locality corresponding to their size

In this scenario according to the linear regression concept:
1. The price of the house is the dependent variable(y)
2. The price per square foot is the independent variable(X)

Linear Regression Concept

Using the linear regression concept the relationship model between the house price and square foot can be determined as:

Where:
1. β0 is the intercept, representing the estimated price of the house when the square foot is 0. Consider it like other facilities that you get with the house
2. β1 is the coefficient, representing the amount by which the price will increase if the number of square foot also increases

This is a simple example of linear regression, where the goal is to find the best-fitting line that predicts the dependent variable (house price) based on the independent variable (square footage).

Types of Linear Regression

Simple Linear Regression

The above example is the best interpretation of the simple linear regression model. It can be defined as the linear regression model where there is only one independent variable and it affects the dependent model most.

A simple linear regression model can be written as:

Here y is the dependent variable based on the independent variable x with a as coefficient and b as intercept.

Multiple Linear Regression

It can be defined as a linear regression model where multiple independent variables are involved in predicting the dependent variable.

A multiple linear regression model can be written as:

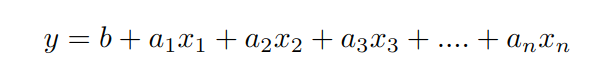
Here y is the dependent variable based on independent variables (x1, x2, x3,…) with (a1, a2, a3,…) as coefficient and b as intercept

Applications:

• Predictive Modeling: Linear regression is widely used in predicting outcomes based on historical data.

• Trend Analysis: It helps in identifying trends and relationships in datasets.

• Feature Impact: It allows us to understand the impact of each independent variable on the dependent variable.

Linear regression is foundational in both statistics and machine learning, serving as a starting point for more complex models.